Math Cheat Sheet for Trigonometry This website uses cookies to ensure you get the best experienceYou have seen quite a few trigonometric identities in the past few pages It is convenient to have a summary of them for reference These identities mostly refer to one angle denoted θ, but there are some that involve two angles, and for those, the two angles are denoted α and β The more important identitiesTrigonometric Identities In this unit we are going to look at trigonometric identities and how to use them to solve tan2 A1=sec2 A Thisisanotherimportantidentity Key Point tan2 A1=sec2 A Onceagain,returningto sin 2Acos A =1 wecandividethroughbysin2 A togive

Trigonometric Identities Edexcel A Level Maths Pure Revision Notes
Tan^2 trig identity
Tan^2 trig identity-Trig identities tan^2Trigonometric Identities Pythagoras's theorem sin2 cos2 = 1 (1) 1 cot2 = cosec2 (2) tan2 1 = sec2 (3) Note that (2) = (1)=sin 2 and (3) = (1)=cos CompoundThe half‐angle identity for tangent can be written in three different forms In the first form, the sign is determined by the quadrant in which the angle α/2 is located Example 5 Verify the identity Example 6 Verify We have certain trigonometric identities Like sin 2 θ cos 2 θ = 1 and 1 tan 2 θ = sec 2 θ etc Such identities are identities in the sense that they hold for all value of the angles which satisfy the given condition among them and they are called conditional identities



Http Faculty Atu Edu Mfinan 13 Lecture18 Pdf
2 x I started this by making sec 1/cos and using the double angle identity for that and it didn't work at all in any way ever Not sure why I can't do that, but something was wrong Anyways I looked at the solutions manual and they magic out 1 tan x tan 2 x = 1 tanMathematics Revision Guides – Further Trigonometric Identities and Equations Page 7 of 17 Author Mark Kudlowski Example (5) Use the result of the previous example to express cos 2A in terms of tan A Since A A A cos2 sin2 tan2 , it follows that A A A tan2 sin2 cos2 A A A tan 2 1 cos 2 sin 2 cos 2A A A A A 2tan 1 tan 1 tanTrigonometry Identities Quotient Identities tan𝜃=sin𝜃 cos𝜃 cot𝜃=cos𝜃 sin𝜃 Reciprocal Identities csc𝜃= 1 sin𝜃 sec𝜃= 1 cos𝜃 cot𝜃= 1 tan𝜃 Pythagorean Identities sin2𝜃cos2𝜃=1 tan 2𝜃1=sec2𝜃 1cot2𝜃=csc2𝜃 Sum & Difference Identities sin( )=sin cos cos sin
Cot (x) = cot (x) sin 2 (x) cos 2 (x) = 1 tan 2 (x) 1 = sec 2 (x) cot 2 (x) 1 = csc 2 (x) sin (x y) = sin x cos y cos x sin y cos (x y) = cos x cosy sin x sin y tan (x y) = (tan x tan y) / (1 tan x tan y) sin (2x) = 2 sin x cos x cos (2x) = cos 2 (x) sin 2 (x) = 2 cos 2 (x) 1 = 1 2 sin 2 (x)Identities involving trig functions are listed below Pythagorean Identities sin 2 θ cos 2 θ = 1 tan 2 θ 1 = sec 2 θ cot 2 θ 1 = csc 2 θ Reciprocal IdentitiesTrigonometricidentitycalculator Prove tan^{2} x * sin^{2} x = tan^{2} x sin^{2} x en
EDIT check out part 2 of this series here!PDF Trigonometric identities are mathematical equations which are made up of functions These identities are true for any value of the variable put There are many identities which are derived by the basic functions, ie, sin, cos, tan, etc The most basic identity is the Pythagorean Identity, which is derived from the Pythagoras TheoremThe trigonometric identities act in a similar manner to multiple passports—there are many ways to represent the same trigonometric expression Just as a spy will choose an Italian passport when traveling to Italy, we choose the identity that applies to the given scenario when solving a trigonometric equation
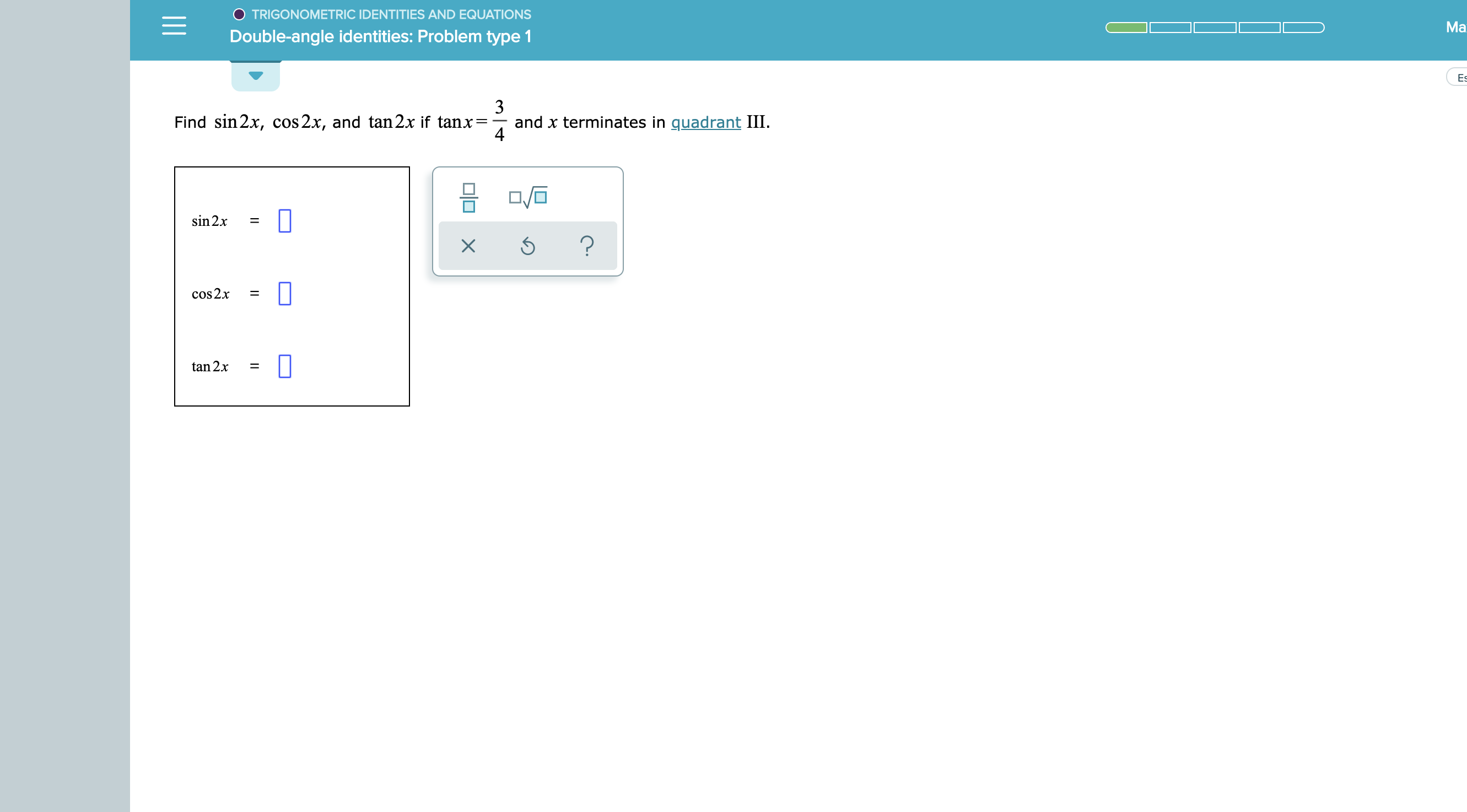



Answered O Trigonometric Identities And Bartleby




Trig Identities Study Sheet
The key Pythagorean Trigonometric identity are sin2(t) cos2(t) = 1 tan2(t) 1 = sec2(t) 1 cot2(t) = csc2(t)Trig identities or a trig substitution mcTYintusingtrig091 Some integrals involving trigonometric functions can be evaluated by using the trigonometric identities These allow the integrand to be written in an alternative form which may be more amenable to integrationThen use the substitution = (), also use the Pythagorean trigonometric identity 1 − sin 2 arctan ( x ) = 1 tan 2 arctan ( x ) 1 {\displaystyle 1\sin ^{2}\arctan(x)={\frac {1}{\tan ^{2}\arctan(x)1}}}



Http Www Humbleisd Net Cms Lib2 Tx Centricity Domain 2966 Chapter 9 1 9 4 notes key Pdf




Sample Problems Cos 2 X Tan2 X Tan 2 Csc 2 Tan Sec X Tan X Cos X Sin 4 X Cos 4 X 1 2 Cos 2 X Pdf Free Download
In this post, I aim to show you guys how to prove all of the formulas, so that if you ever forget one formula, you can just prove it again!Various identities and properties essential in trigonometry Legend x and y are independent variables, d is the differential operator, int is the integration operator, C is the constant of integration Identities tan x = sin x /cos x equation 1The Pythagorean identities are based on the properties of a right triangle cos2θsin2θ =1 1tan2θ =sec2θ 1cot2θ =csc2θ cos 2 θ sin 2 θ = 1 1 tan 2 θ = sec 2 θ 1 cot 2 θ = csc 2 θ The evenodd identities relate the value of a trigonometric function at a given angle to the value of the function at the opposite angle




Integration Using Trigonometric Identities 2 Examsolutions Youtube




Reciprocal Identities In Trigonometry With Examples Owlcation
We recall the Pythagorean trig identity, and multiply the angles by 2 throughout to keep the equation in balance We rearrange the trig identity for sin 2 2x We divide throughout by cos 2 2x The LHS becomes tan 2 2x, which is our integration problem, and can be expressed in a different form shown on the RHS However, we still need to make some changes to the first term on the Verifying Trigonometric Identities Now that you are comfortable simplifying expressions, we will extend the idea to verifying entire identities Here are a few helpful hints to verify an identity Change everything into terms of sine and cosine Use the identities when you can Start with simplifying the lefthand side of the equation, then$\tan^2{\theta} \,=\, \sec^2{\theta}1$ The square of tan function equals to the subtraction of one from the square of secant function is called the tan squared formula It is also called as the square of tan function identity Introduction The tangent functions are often involved in trigonometric expressions and equations in square form The expressions or equations can be possibly simplified by transforming the tan




Trigonometric Identities Edexcel A Level Maths Pure Revision Notes




Basic Trigonometric Identities And Equations Ppt Download
Hence, this post shows you a figure you can use to remember the reciprocal, quotient, and Pythagorean identities Trigonometric Identities Sine, tangent, cotangent and cosecant in mathematics an identity is an equation that is always true Meanwhile trigonometric identities are equations that involve trigonometric functions that are always true This identitiesTrigonometric identities are equations that relate different trigonometric functions and are true for any value of the variable that is there in the domainBasically, an identity is an equation that holds true for all the values of the variable(s) present in it




最も人気のある Tan2 Identity ただの悪魔の画像



3
Hi everyone, Have you ever had a hard time remembering all those Trigonometric Identities, like the cosine angle sum, or sine angle difference, or half angle formulas?Trigonometricidentityprovingcalculator prove \tan^2(x)\sin^2(x)=\tan^2(x)\sin^2(x) enTwo New Identities So, we started out in the Basic Trig Identities section by forming the identity \sin ^2 \theta \cos ^2 \theta \equiv 1 From there, we can derive two new ones Identity 1




How Do You Prove Tan 2x Secx 1 1 Secx Socratic



Www2 Math Binghamton Edu Lib Exe Fetch Php People Mckenzie Trig Identities Worksheet With Answers 2 Pdf
I'm working on a problem but it's been a while since I last saw trig identities so I'd love some help or being pointed in the right direction Basically, I'd like to understand where this identity comes from; 1 Answer sente Using the following tan(x) = sin(x) cos(x) cos2(x) sin2(x) = 1 sec(x) = 1 cos(x) for cos(x) ≠ 0, we have 1 tan21tan2 a = sec2 a As it is known that tan a is not defined for a = 90° therefore identity 2 obtained above is true for 0 ≤ A
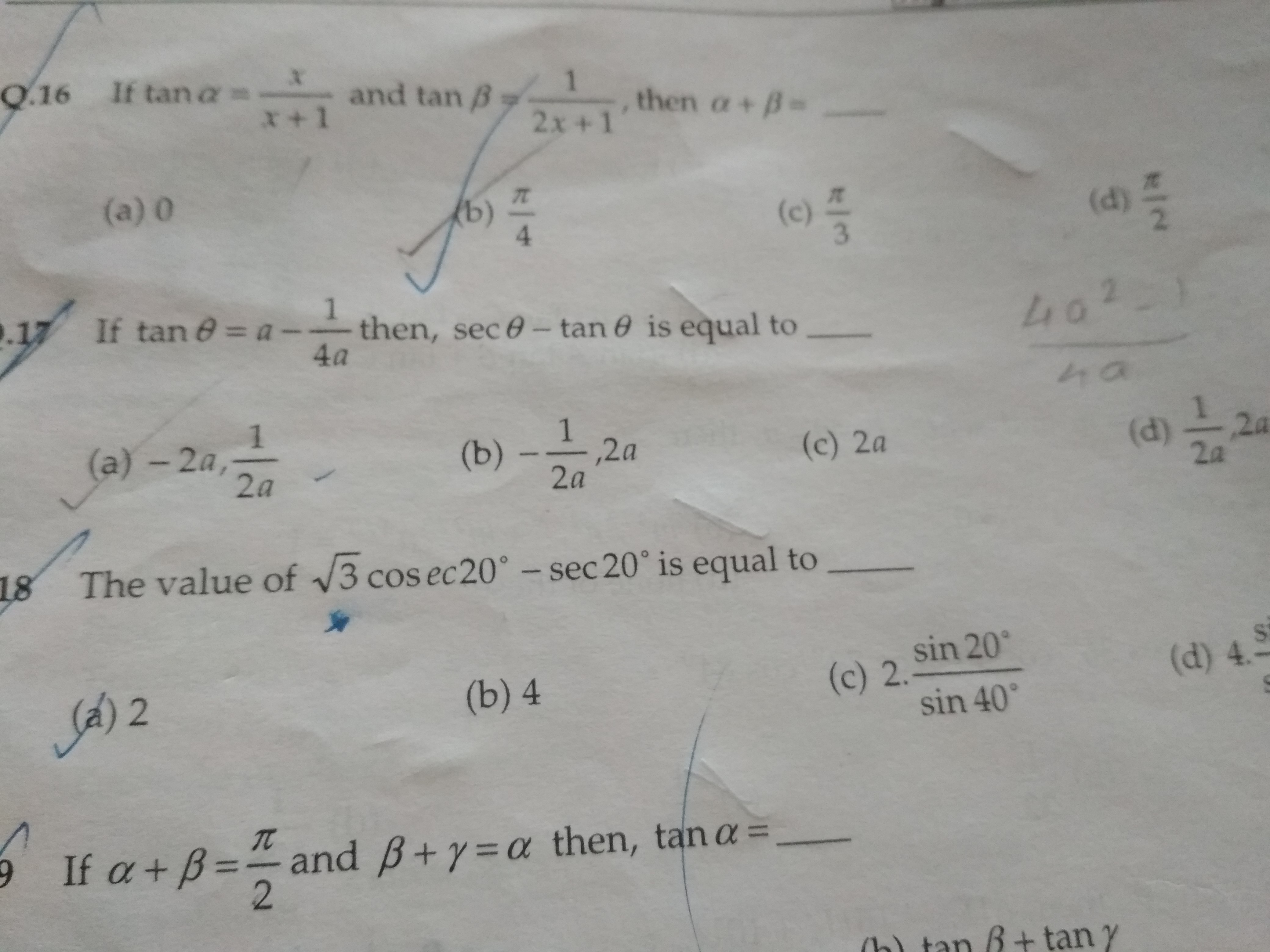



Trigonometric Identities Questions And Answers Topperlearning
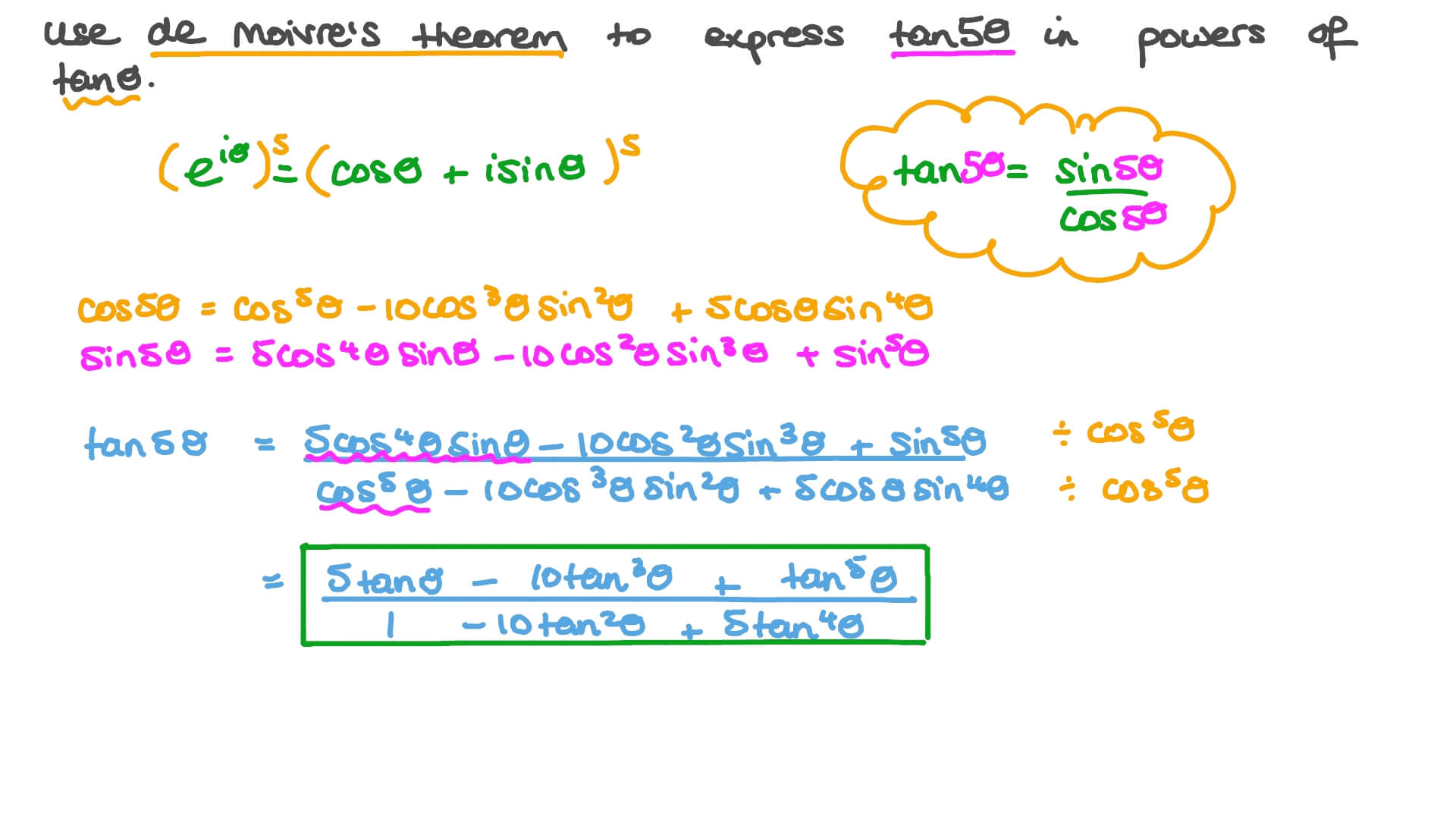



Question Video Using De Moivre S Theorem To Derive Trigonometric Identities Nagwa
Recall A trigonometric identity is an equation formed by the equivalence of two trigonometric expressions The solution to the equation must be the set of all values of the variable, in which both expressions are defined Examples Example 1 Consider the trigonometric equationTan (2x) = 2 tan (x) / (1 tan ^2 (x)) sin ^2 (x) = 1/2 1/2 cos (2x) cos ^2 (x) = 1/2 1/2 cos (2x) sin x sin y = 2 sin ( (x y)/2 ) cos ( (x y)/2 ) cos x cos y = 2 sin ( (x y)/2 ) sin ( (x y)/2 ) Trig Table of Common Angles angleTrigonometric Identities mcTYtrigids091 In this unit we are going to look at trigonometric identities and how to use them to solve trigonometric equations In order to master the techniques explained here it is vital that you undertake plenty of practice exercises so



Http Faculty Atu Edu Mfinan 13 Lecture18 Pdf




Tan 2x Formula What Is Tan 2x Formula Examples
Using Trig Identities to Solve a Quadratic in Sin x Category Mathematics In the first of this pair of Casio videos, the identity sin 2 x cos 2 x≡ 1 is used to solve fully the equation 9sin 2 x 21sinx = 3cos 2 x 12 The second video explores how a graphical calculator can be used to find solutions of the equation by plotting both sides of the equation we are trying to solve, and Here we will prove the problems on trigonometric identities As you know that the identity consists of two sides in equation, named Left Hand Side (abbreviated as LHS) and Right Hand Side (abbreviated as RHS)To prove the identity, sometimes we need to apply more fundamental identities, eg $\sin^2 x \cos^2 x = 1$ and use logical steps in order to lead oneJoin this channel to get access to perkshttps//wwwyoutubecom/channel/UCFhqELShDKKPv0JRCDQgFoQ/joinHere is the technique to solve this integration and how
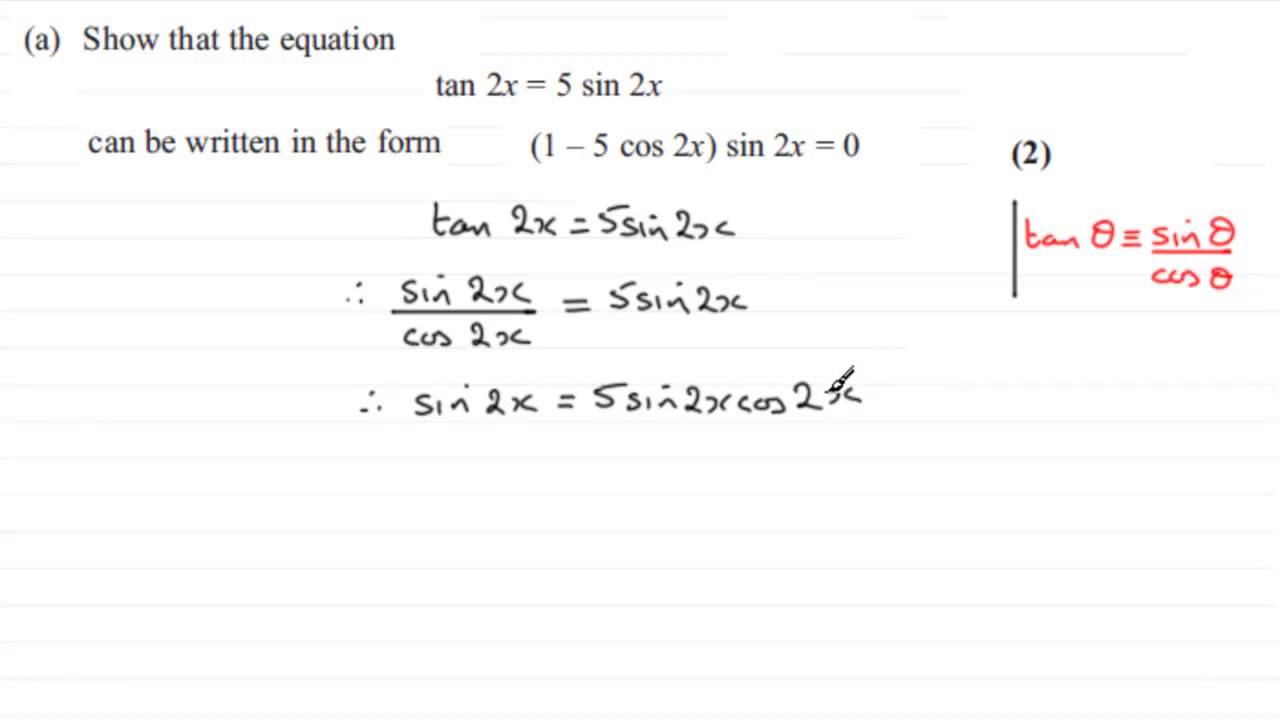



Exam Questions Trigonometric Identities Examsolutions



Solved Prove The Following Trig Identities Course Hero
2 The Elementary Identities Let (x;y) be the point on the unit circle centered at (0;0) that determines the angletrad Recall that the de nitions of the trigonometric functions for this angle are sint = y tant = y x sect = 1 y cost = x cott = x y csct = 1 x These de nitions readily establish the rst of the elementary or fundamental identities given in the table belowLet's start with the left side since it has more going on Using basic trig identities, we know tan (θ) can be converted to sin (θ)/ cos (θ), which makes everything sines and cosines 1 − c o s ( 2 θ) = ( s i n ( θ) c o s ( θ) ) s i n ( 2 θ) Distribute the right side of the equation 1 − c o s ( 2 θ) = 2 s i n 2 ( θ) A trigonometric identity is an equality between two expressions Furthermore, these expressions usually involve trigonometric functions Because of many identities, it can be hard to remember the essentials;
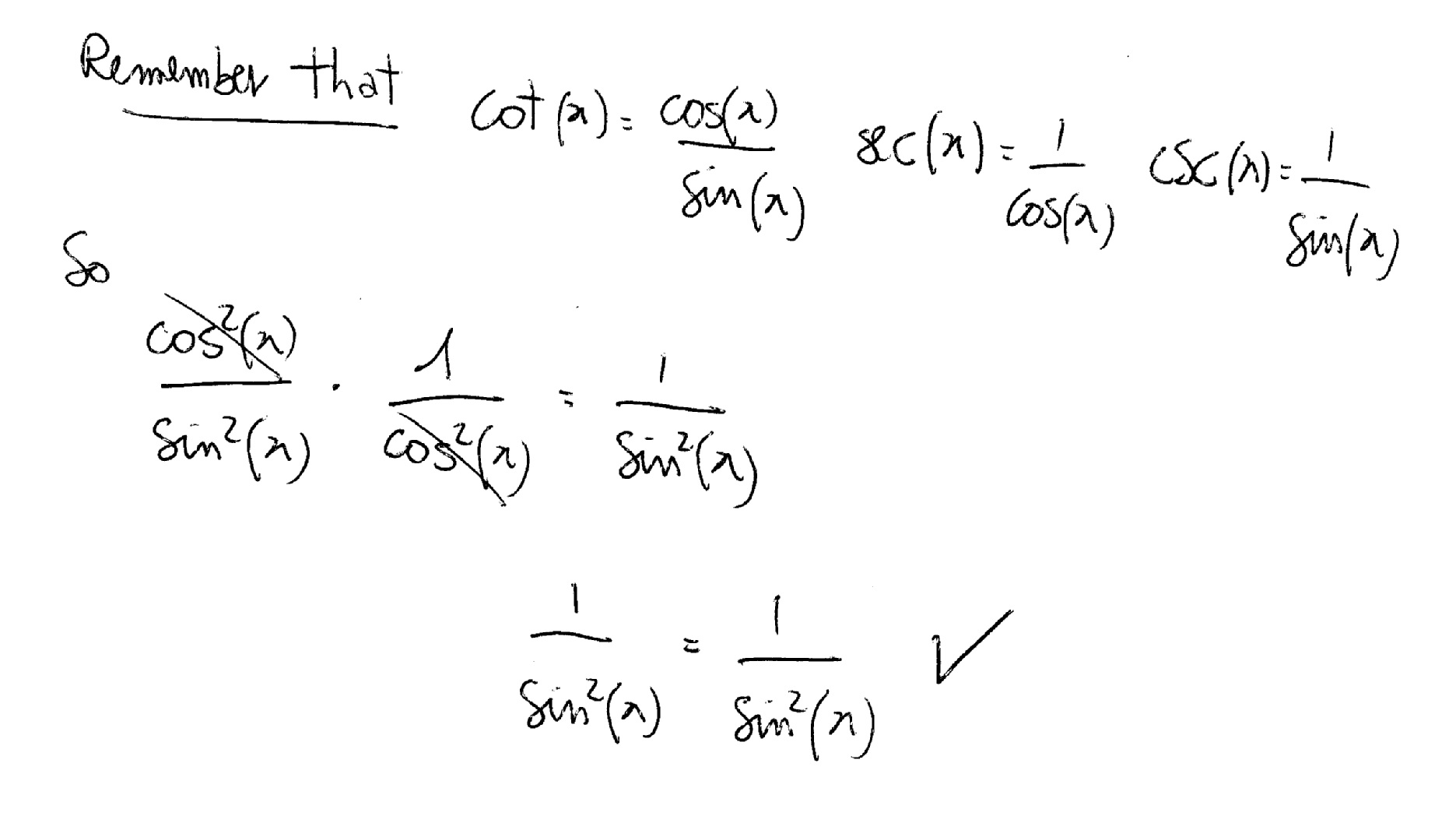



How Do You Verify Cot 2x Sec 2x Csc 2x Socratic




Trigonometric Identities Math Forums
The trigonometric identities act in a similar manner to multiple passports—there are many ways to represent the same trigonometric expression Just as a spy will choose an Italian passport when traveling to Italy, we choose the identity that applies to the given scenario when solving a trigonometric equation$$\tan(2t) = \dfrac{2\tan(t)}{1 \tan^2(t)}$$ Thanks for any help you can give if it's useful to know the context of the problem, I'mTrig Equations and Identities wwwnaikermathscom 4 (a) Given that sin q = 5 cos q, find the value of tan q (1) (b) Hence, or otherwise, find the values of q in the interval 0 £ q < 360° for which sin q = 5 cos q, giving your answers to 1 decimal place (3) June 06 Q6 5 (a) Show that the equation 3 sin2 q – 2 cos2 q = 1 can be written as
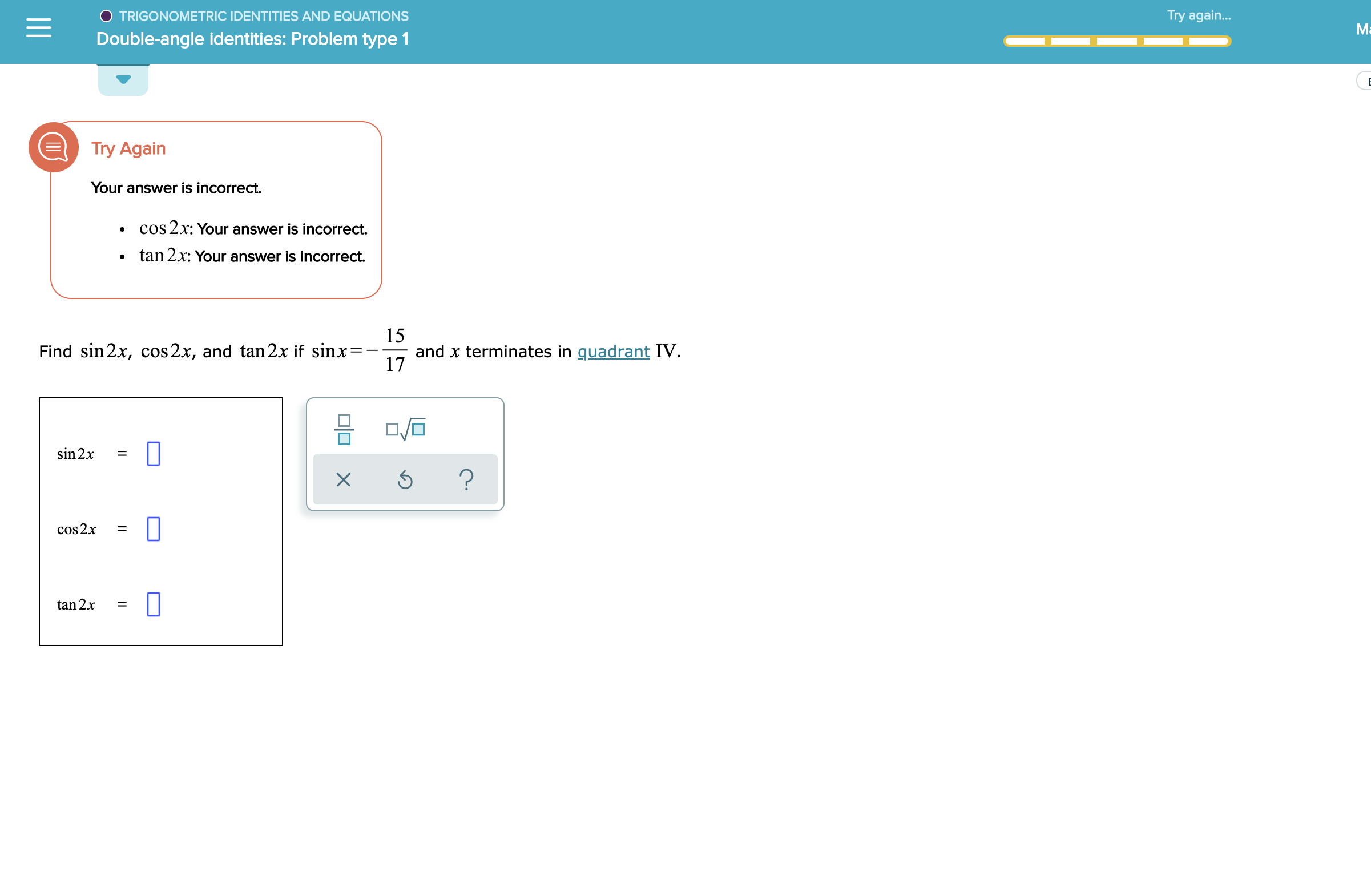



Answered O Trigonometric Identities And Bartleby



Mi Schoolwires Net Cms Lib Mi Centricity Domain 433 Trig identities notes and hw packet march 18 Pdf
62 Trigonometric identities (EMBHH) An identity is a mathematical statement that equates one quantity with another Trigonometric identities allow us to simplify a given expression so that it contains sine and cosine ratios only This enables us to solve equations and also to prove other identitiesUse trigonometric identities to show that mc = abcos(ω ct)cos(u mt) = k 1 cos((ω c −u m)t)k 2 cos((ω c u m)t) where k 1 and k 2 are constants Then substitute ω c = 2×106 ×2π and ω m = 0×2π to calculate the two resulting frequencies (b) Use trigonometric identities to show that multiplying the modulated signal by bcos(u ct) resultsA trigonometric identity in one variable is an equality that involves trigonometric functions and is true for all values of the variable for which both sides of the equality are defined Recall the Pythagorean theorem that relates the lengths of the sides of a right triangle \{a^2} {b^2} = {c^2},\ where \(a,b\) are the lengths of the triangle's legs and \(c\) is the length of its




Trigonometry By Brandon Soto



Stmchs Learning Powerschool Com Rpolicar Introcalculus Cms File Show 2549 Pdf T
Simplify tan^2 x sec^2 Ans 1 Use trig identity 1 tan^2 x = sec^2 x tan^2 x sec^2 x = 1 Here are sixteen Trigonometric Identities SIN = Sine COS = Cosine TAN = Tangent CSC = CoSecant SEC = Secant COT = CoTangent #1 1 SIN Θ = CSC Θ #2 1 COS Θ = SEC Θ #3 SIN Θ TAN Θ = COS Θ #4 COS Θ 1 COT Θ = = SIN Θ TAN Θ #5 1 SEC Θ = COS Θ #6 1 CSC Θ = SIN Θ #7 SIN 2 Θ COS 2 Θ = 1 #8 SEC 2 Θ = 1 TAN 2 Θ #9 CSCTrigonometry Identity tan^2 (x) 1 = sec^2 (x) Watch later Share Copy link Info Shopping Tap to unmute If playback doesn't begin shortly, try restarting your device Up next in 8




Trigonometric Identities




Inquiry 11 8 Marks Prove The Following Trig Chegg Com
Trig Identities Cheat Sheet admin When solving, simplify with the identities initially, if you can Trigonometric identities are used to manipulate the trigonometric equations of some specific forms In this video, the Pythagorean identities and the way they are derived are shown In mathematics, there are numerous logarithmic




Trigonometry Identities And Equations Ppt Download
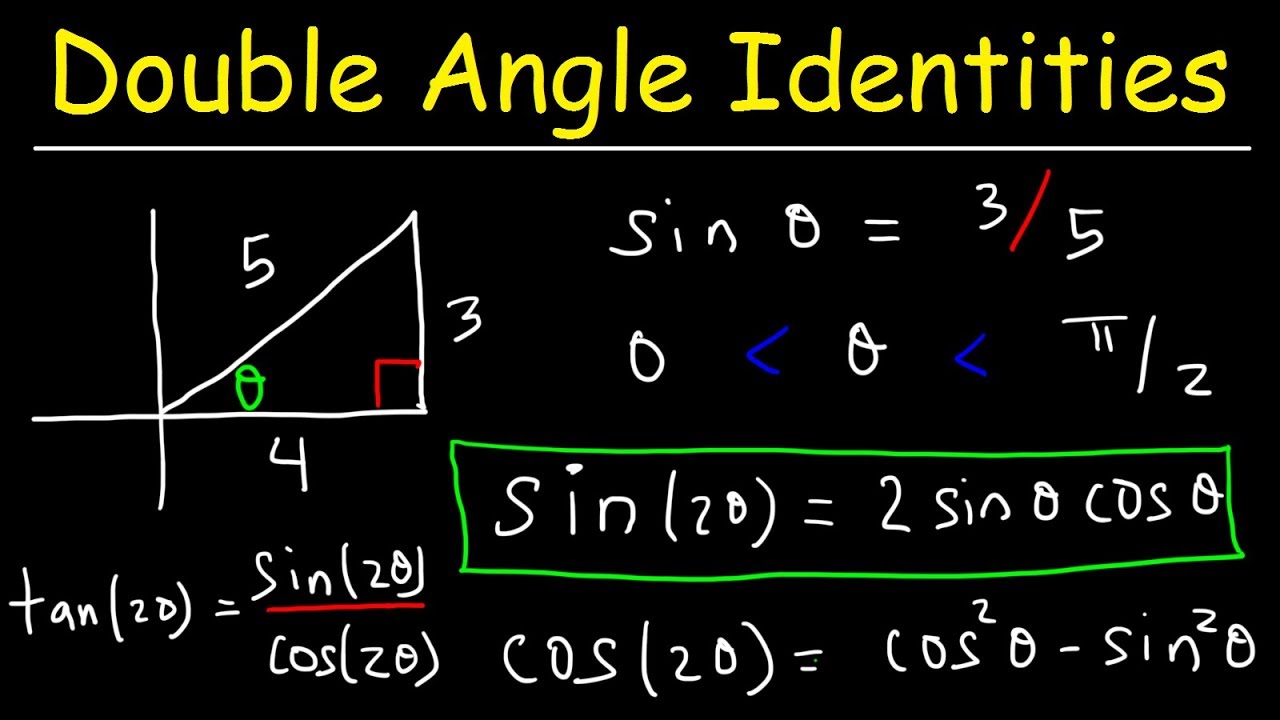



Double Angle Identities Formulas Of Sin Cos Tan Trigonometry Youtube




Trigonometric Identities Trigonometric Functions Trigonometry



Http Www Whsd K12 Pa Us Userfiles 1598 Classes 9713 Trig chapter 5 notes Pdf




Tan 2x Csc 2x Tan 2x 1 Problem Solving Solving Identity



2




7 Prove One Of The Following Trigonometric Identi Gauthmath




Trigonometric Identities




Unit 6 Challenge Problems Sine Trigonometry




B Prove The Following Trigonometric Identities I Gauthmath




Trig Identities All List Of Trigonometric Identities Learn Trigonometry




Double Angle Identities Formulas Of Sin Cos Tan Trigonometry Youtube




Double Angle Identities Joke Worksheet Math Love



Http Www Mrsfruge Com Uploads 1 2 0 0 Precalculus Chapter 5 Packet Answers Pdf



Www Brockport Edu Academics Tutoring Docs Trigonometric Identities Pdf




Trigonometry Laws And Identities Tool Eeweb Community




Trigonometric Identity Examples Solutions Videos
.JPG)



Every Day I M Calculatin I D3 Unit Q Pythagorean Identities



Www Washoeschools Net Site Handlers Filedownload Ashx Moduleinstanceid Dataid Filename Chapter 5 teacher notes Pdf




Reciprocal Identities In Trigonometry With Examples Owlcation



1




Verifying Trigonometric Identities Sec 7 1 Trigonometric Expression Identity




Grade 12 Trigonometry Sum Or Difference Identity Homeworkhelp



Common Identities Properties Of Trigonometric Functions 4 8 Sideway Output To




Verifying A Trigonometric Identity Tan 2 X 1 Sec X Sec X Youtube



Trigonometric Identity Example Proof Involving Sin Cos And Tan Video Khan Academy




Cos Sin Tan Csc Sec Cot
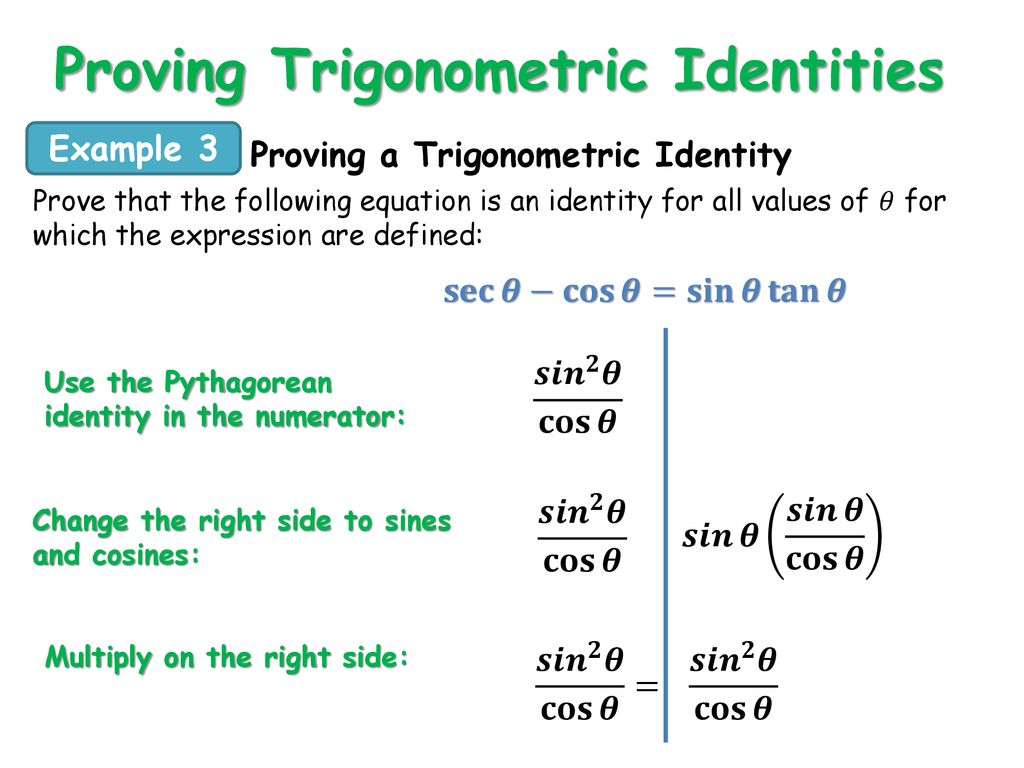



Trigonometry Identities And Equations Ppt Download




Cos Sin Tan Csc Sec Cot




Trig Identities Worksheet With Answers 2



Trig Identities Crossword Wordmint




Sample Problems Cos 2 X Tan2 X Tan 2 Csc 2 Tan Sec X Tan X Cos X Sin 4 X Cos 4 X 1 2 Cos 2 X Pdf Free Download




How Do You Prove The Identity Tan 2x Secx 1 1 Cosx Cosx Socratic




Check My Work Evaluating Tan Frac 7 Pi 8 Using A Half Angle Formula Mathematics Stack Exchange




List Of Trigonometric Identities Wikipedia




7 3a Trigonometry Part Ii Questions Trigonometric Functions Sine




Identities For Sin2a Cos2a And Tan2a Examsolutions



Http Www Math Wsu Edu Faculty Cjacobs 108 108 6 1handout Pdf




Trigonometric Identities Sin Cos And Tan Mr Mathematics Com




Trig Identities Table Of Trigonometric Identities




Trigonometric Identities Edexcel A Level Maths Pure Revision Notes




What Is Quotient Identity Know It Info




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo




Sample Problems Cos 2 X Tan2 X Tan 2 Csc 2 Tan Sec X Tan X Cos X Sin 4 X Cos 4 X 1 2 Cos 2 X Pdf Free Download




Cos Sin Tan Csc Sec Cot




Ppt Analytic Trig Powerpoint Presentation Free Download Id




Using Basic Trigonometric Identities Simplify The Following Expression Cos 0 Cot 0 Tan 0 Cos 0 Brainly Com



Www Usna Edu Users Physics Tank Other Mathmethods Triggeometry Trighandout30jun11 Pdf




Precalculus Trigonometry Trig Identities 47 Of 57 Solve Tan 2 Theta 4 0 Theta Youtube



1




Trig Identities Maple Learn Maplesoft




Trigonometric Identity Example Proof Involving All The Six Ratios Video Khan Academy




Ppt Warm Up Powerpoint Presentation Free Download Id



Www2 Math Binghamton Edu Lib Exe Fetch Php People Mckenzie Trig Identities Worksheet With Answers 2 Pdf




Trigonometry Identity Tan 2 X 1 Sec 2 X Youtube




Trigonometric Identities A Plus Topper




Prove The Following Trigonometric Identities Show Gauthmath




Cofunction Identities In Trigonometry With Proof And Examples Owlcation




Algebra 2 Simple Trigonometry Identity Simplifications And Proofs I Have Attempted 11 16 And Simply Cannot Understand How They Are Getting Those Answers If Someone Could Explain One Of Them Maybe I Will



Web Stanford Edu Class Archive Math Math Math 1144 Files Trig Pdf




How Do You Verify 4tan 4 Tan 2x 3 Sec 2x 4tan 2x 3 Kinda Hard Please With All The Steps Thanks Socratic




Powers Of Trigonometric Functions




Microsoft Word A 3 1 Basic 8 Trig Identities Sine Trigonometric Functions



Www Math Uci Edu ronc8 Trig Ids Pdf




Trigonometric Identities Practice Problems Key



3
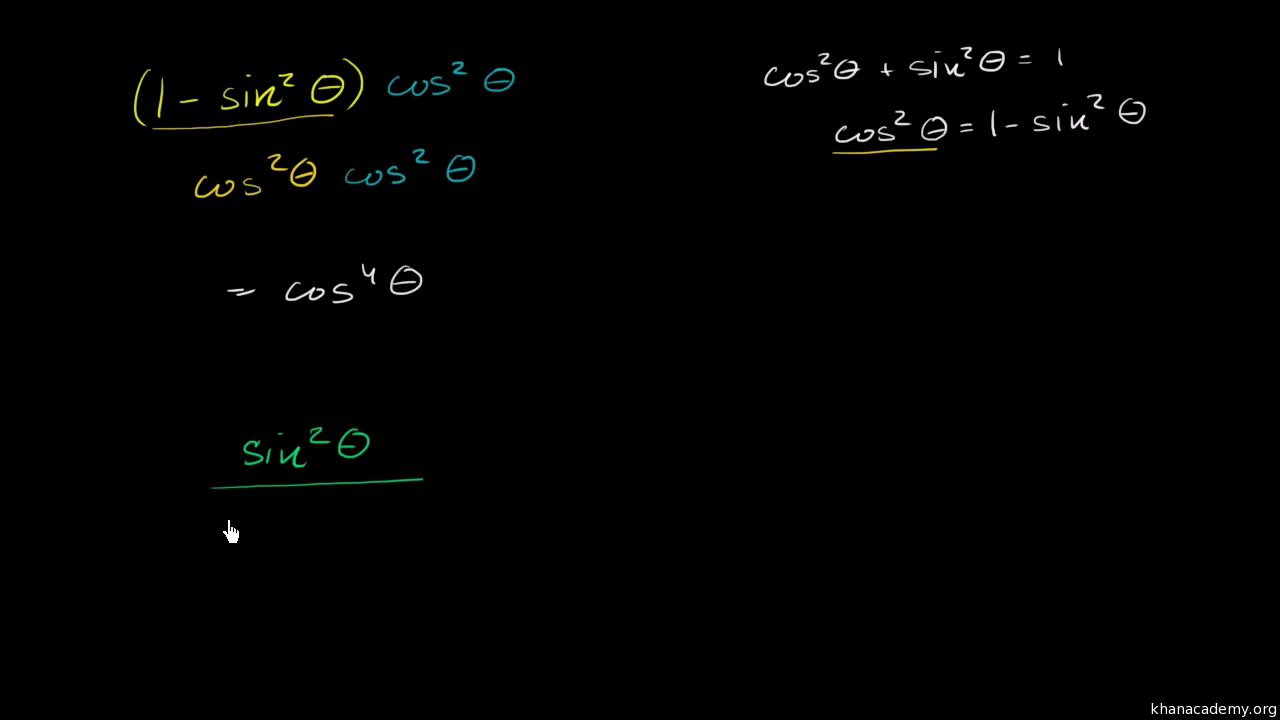



Using Trigonometric Identities Video Khan Academy




The Reciprocal Trigonometric Functions Problem 3 Trigonometry Video By Brightstorm




Verify The Trigonometric Identity 1 1 Sin 2 X 1 Tan 2 X In 21 Identity Sins Math



Solved Prove The Following Trig Identity Sec 2 X 2secx Cosx Cos 2 X Tan 2 X Sin 2 X Course Hero




5 1 5 2 Trigonometric Identities Ppt Download




Trigonometric Identities Youtube



Edumaterial Casio Intl Com Resource Contents 91




Solved Inquiry 11 8 Marks Prove The Following Trig Iden Chegg Com




Trigonometric Identities Sin Cos And Tan Mr Mathematics Com




Cos Sin Tan Csc Sec Cot




Trigonometric Identities Sin 2 X Cos 2 X Tan 2 X Youtube




Advanced Trigonometric Identities Solutions Examples Videos



0 件のコメント:
コメントを投稿